






































https://github.com/byumm315/streamlit_diamonds/tree/master
GitHub - byumm315/streamlit_diamonds
Contribute to byumm315/streamlit_diamonds development by creating an account on GitHub.
github.com
https://appdiamonds-1gov6bbrlv8.streamlit.app/
Home
This app was built in Streamlit! Check it out and visit https://streamlit.io for more awesome community apps. 🎈
appdiamonds-1gov6bbrlv8.streamlit.app
코드 오류시 댓글로 남겨주세요.
https://github.com/byumm315/tweeter_cleaner
GitHub - byumm315/tweeter_cleaner: tweeter_cleaner using python3 // Selenium, Pyautogui
tweeter_cleaner using python3 // Selenium, Pyautogui - GitHub - byumm315/tweeter_cleaner: tweeter_cleaner using python3 // Selenium, Pyautogui
github.com
<내가 쓴 트윗 지우기 영상>
<알티한 게시글 지우기 영상>
Hyper Parameter는 모델 학습 과정을 제어하기 위해 사용하는 파라미터입니다.
Hyper Parameter 탐색 방법에는 대표적으로 Grid Search, Random Search 방법이 있습니다.
이 탐색 방법들의 문제점을 해결하기 위해 Hyper Parameter 최적화를 이용합니다.
Hyper Parameter 최적화는 대표적으로 Bayesian 최적화가 있습니다.
우선 Hyper Parameter 최적화는 Black-box Optimization으로, Hyper Parameter가 입력값, 출력값은 Loss일때 둘 사이의 관계를 미리 수식으로 표현할 수 없습니다.
즉, Objective Function을 알 수 없습니다. 그래서 Gradient를 계산할 수 없습니다.
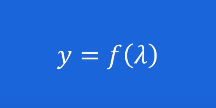
[그림1]에서 lambda는 Hyper Parameter, y는 Loss, f()는 Objective Function이 되겠습니다.
1) 관측 데이터를 기반으로 f(x)를 추정합니다.
- Bayes 정리를 활용
- Gaussian Process -> f(x)를 평균과 분산이라는 개념으로 선택함
2) 추정 모델을 기반으로 탐색할 파라미터를 선택합니다.
- 평균이 큰것(Exploitation)
- 분산이 큰것(Exploration)
Bayesian 최적화는 기본적으로 Surrogate Function과 Acquisition Function으로 구성됩니다.
실제로 관측한 값들을 기반으로 미지의 Objective Function 형태에 대한 확률적인 추정을 수행하는 함수입니다.
임의의 Hyper Parameter set을 입력하면 그때 예측된 Objective Function으로 구한 Loss 평균과 분산을 출력합니다.
이때, Gaussian Processes를 이용합니다.
Gaussian Process는 정규분포를 기반으로 합니다.
- 분포: 하나의 변수를 사용할때의 용어
- Process: 하나의 함수를 사용할때의 용어

분산함수 추정을 위해 Matern 5/2 Kernel을 이용합니다. ([그림2]의 식에서는 Kernel이라고 합니다)
d(lambda, lambda*)은 서로 다른 두 Hyper Parameter Set간의 거리를 의미합니다.
Matern 5/2 Kernel을 이용해 평균 함수(M(lambda))와 분산 함수(Sigma^2(lambda))를 구합니다.
Surrogate Function이 만들어져 평균 함수(M(lambda))와 표준편차 함수(Sigma(lambda))를 알 수 있다고 가정합시다.
이때, Acquisition Function은 Exploration과 Exploitation을 고려해서 최적의 다음 Hyper Paramter Set을 찾는 함수입니다.
Exploitation: 평균이 큰 것을 의미합니다.
Exploration: 분산이 큰 것을 의미합니다.

[그림3]의 E[I]는 Expected Improvment로 현재까지 가장 좋은 Loss와 평균의 차이로 구성된 함수입니다.
여기서 파이와 로우는 정규분포입니다.
f min 은 실제 관측된 값들 중에서 가장 낮은 Loss를 의미합니다.
즉 E[I]를 해석하자면, 실제로 가장 낮은 Loss와 추정된 Loss의 평균 차이를 기반으로 Acquisition Function을 구하는 것입니다.
E[I]가 가장 큰 값을 직관적으로 해석하면, 실제로 가장 낮은 Loss와 추정된 Loss의 평균의 차이가 가장 큰 값을 의미합니다.
따라서 우리는 Acquisition Function을 통해 E[I]가 가장 큰 값을 구합니다.
이후, 해당 Hyper Parameter Set을 다음 Hyper Parameter Set으로 반영하는 것입니다.
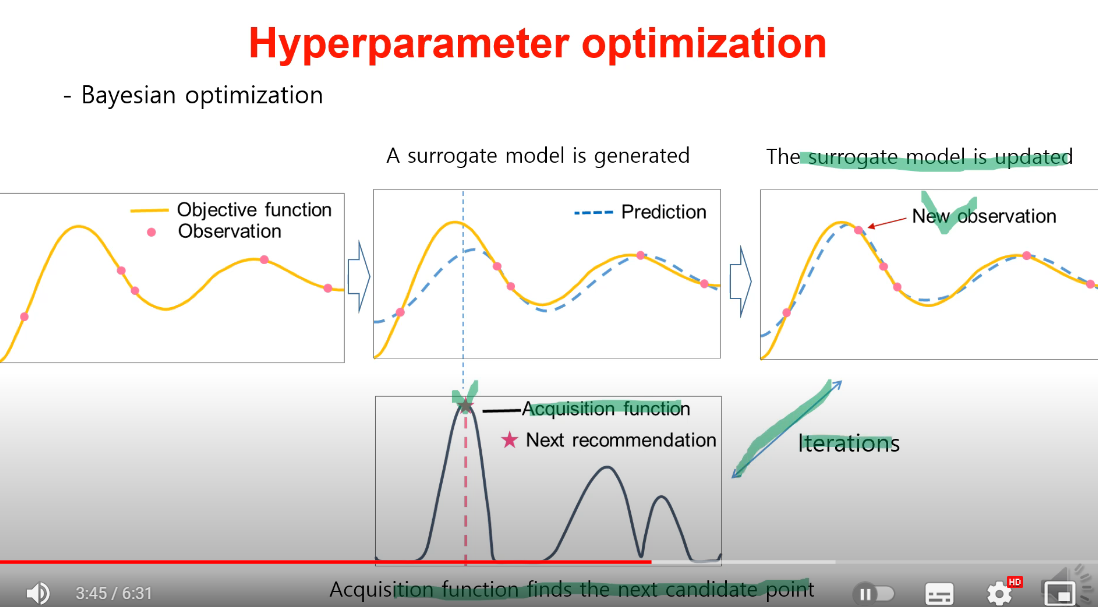
[그림4]를 참고하여 과정을 정리해보겠습니다.
1) Observation 몇개를 기반으로 미지의 Objection Function(Black Box)을 추정합니다.
2) Objective Function과 관측값을 기반으로 Surrogate Function을 만듭니다.
3) Acquisition Function을 통해 가장 높은 값을 갖는 Hyper Parameter Set을 찾습니다.
4) 새로운 Hyper Parameter Set을 반영해서 다시 Surrogate Model을 업데이트합니다.
5) 3)~4) 과정이 반복되면서 최적의 하이퍼 파라미터를 찾습니다.
출처: https://www.youtube.com/watch?v=mxr8G4hDPcM
출처: https://www.youtube.com/watch?v=w9D8ozS0oC4
출처: https://www.youtube.com/watch?v=PTxqPfG_lXY
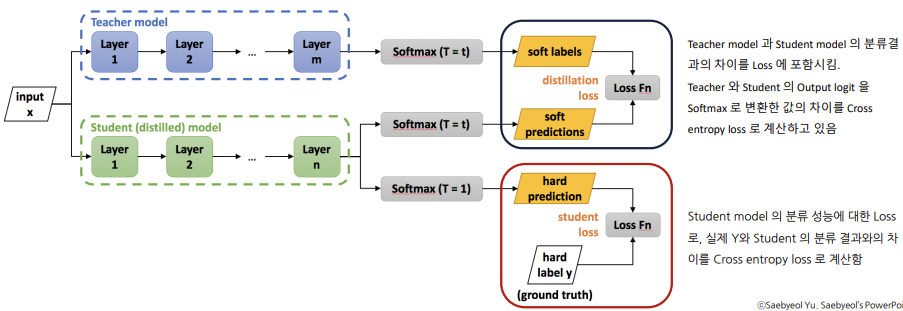
잘 학습된 Teacher 모델의 지식을 전달하여 단순한 Student 모델로 비슷한 좋은 성능을 내고자 함
즉, 잘 학습된 Teacher 모델과 잘 학습된 Student 모델을 구한 후, "Student 모델 결과와 실제 Y값의 오차", "Teacher 모델 결과와 Student 모델 결과의 오차"를 활용해 새로운 오차를 구한다.
이 오차를 가장 작게 만드는 모델이 Best Student Model이다.
Teacher 모델: 높은 예측 정확도를 가진 복잡한 모델
Student 모델: Teacher 모델의 지식을 받는 단순한 모델
대회 정보: https://dacon.io/competitions/official/236013/overview/description
문제 상황: Train data의 변수는 40여개였으나, Test data의 변수는 16개 가량 있었음
1. Train data와 Test data를 Tensor 형태로 바꾸고 Mini batch size 256개로 묶어서 여러개의 덩어리(train_loader, val_loader, test_loader)를 만들었음
- 이 과정에서 train_dataset, val_dataset, test_dataset 생성함
1) train_dataset은 train_X, train_y에서 전체 X변수가 있는 teacher_X와 16개의 일부 X변수가 있는 student_X 그리고 y로 변화함
2) val_dataset은 val_X, val_y에서 전체 X변수가 있는 teacher_X와 16개의 일부 X변수가 있는 student_X 그리고 y로 변화함
3) test_dataset은 test_X에서 16개의 일부 X변수가 있는 student_X로 변화함
[1), 2), 3) 모두 tensor 형태이다]
2. train_loader, val_loader와 teacher_model(레이어가 엄청 많은 신경망 모델)을 이용해서 오차가 가장 작은 teacher model을 만들었음
- train_loader와 val_loader의 teacher_X(전체 X변수를 가짐)를 이용한다.
3. train_loader, val_loader와 student_model(레이어가 작은 신경망 모델)을 이용해서 오차가 가장 작은 student model을 만들었음
- train_loader와 val_loader의 student_X(16개의 일부 X변수를 가짐)를 이용한다.
4. student_model, teacher_model, train_loader, val_loader를 student_train() 함수에 적용해서 best_student_model을 만들었음
- student_train() 함수는 train_loader에서 만들어진 미니배치 덩어리 중 하나에서 student_X를 student_model에 학습한다.
- 이후 만들어진 미니배치 덩어리 중 하나에서 teacher_X를 각각 teacher_model에 학습한다.
- distill_loss() 즉, student_model output과 실제 y값, teacher_model output을 연산해서 distillation 오차를 구한다.
(이 오차는 "student_model output과 teacher_model output간의 BCELoss", "student_model output과 실제 y값간의 BCELOSS" 그리고 alpha를 이용해서 구한 값이다. alpha가 어떤 값이냐에 따라서 distillation 오차가 달라진다.)
- 한 에포크당 val_loss와 val_score(f1 score)를 구하고 에포크당 val_score를 비교해서 best_score와 best_model을 구한다.
5. 최적의 Threshold를 찾은 후, best_student_model()을 이용해서 예측값을 추정한다.
# -*- coding: utf-8 -*-
"""건설기계 오일 상태 분류
Automatically generated by Colaboratory.
Original file is located at
https://colab.research.google.com/drive/1xF84hVt5oIiOOucg-vitK7pcO_wVGwE1
"""
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
"""
PyTorch는 데이터 처리를 위한 두 가지 클래스( torch.utils.data.Dataset 및 torch.utils.data.DataLoader)를 제공 합니다.
Dataset 은 샘플과 정답(label)을 저장합니다.
DataLoader 는 Dataset 을 샘플에 쉽게 접근할 수 있도록 순회 가능한 객체(iterable)로 감쌉니다.
많은 양의 data를 이용해 딥러닝 모델을 학습시킬 때 data를 한번에 불러오면 시간이 오래걸립니다.
데이터를 한번에 다 부르지 않고 하나씩만 불러서 쓰는 방식을 택하면 작은 메모리를 가진 컴퓨터에서도 모델을 돌릴 수 있습니다.
그래서 custom dataset을 만들어야할 필요가 있습니다.
길이가 변하는 input에 대해서 batch를 만들기 위해서는 dataloader에서 batch를 만드는 부분을 수정해야할 필요가 있습니다.
따라서 custom dataloader를 사용해야 합니다.
"""
from torch.utils.data import DataLoader, Dataset
from sklearn.metrics import f1_score
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split
import os
import pandas as pd
import numpy as np
from tqdm.auto import tqdm
import random
import warnings
warnings.filterwarnings(action='ignore')
device = torch.device('cuda') if torch.cuda.is_available() else torch.device('cpu')
CFG = {
'EPOCHS': 30,
'LEARNING_RATE':1e-2,
'BATCH_SIZE':256,
'SEED':41
}
def seed_everything(seed):
random.seed(seed)
os.environ['PYTHONHASHSEED'] = str(seed)
np.random.seed(seed)
torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = True
seed_everything(CFG['SEED'])
from google.colab import drive
drive.mount('/content/drive')
import pandas as pd
train=pd.read_csv('/content/drive/MyDrive/machine_oil/train.csv',sep=',',encoding="cp949")
test=pd.read_csv('/content/drive/MyDrive/machine_oil/test.csv',sep=',',encoding="cp949")
submission=pd.read_csv('/content/drive/MyDrive/machine_oil/sample_submission.csv',sep=',',encoding="cp949")
list(round(np.mean(train[['CD',
'FH2O',
'FNOX',
'FOPTIMETHGLY',
'FOXID',
'FSO4',
'FTBN',
'FUEL',
'K',
'SOOTPERCENTAGE',
'U100',
'U75',
'U50',
'U25',
'U20',
'U14',
'U6',
'U4',
'V100']]),2))
from sklearn.impute import KNNImputer
# create an object for KNNImputer
imputer = KNNImputer(n_neighbors=2)
train_1 = imputer.fit_transform(train.drop(['ID','COMPONENT_ARBITRARY','YEAR'],axis=1))
train_2=pd.DataFrame(train_1,columns=train.drop(['ID','COMPONENT_ARBITRARY','YEAR'],axis=1).columns)
train_2['ID']=train['ID']
train_2['COMPONENT_ARBITRARY']=train['COMPONENT_ARBITRARY']
train_2['YEAR']=train['YEAR']
a=train_2.corr(method='pearson')
aa=pd.DataFrame(a)
for i in range(len(aa)):
for j in range(len(aa.columns)):
if i<j and aa.iloc[i,j]>=0.6:
print(aa.index[i],aa.columns[j])
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca_M = pca.fit_transform(train_2[['FE','MN','SI','NI','TI','V']])
train_2=train_2.drop(['FE','MN','SI','NI','TI','V'],axis=1)
train_2[['M1','M2']]=pca_M
pca = PCA(n_components=2)
pca_U1 = pca.fit_transform(train_2[['U25','U20', 'U14','U6' ,'U4','S']])
pca = PCA(n_components=1)
pca_U2 = pca.fit_transform(train_2[['U100','U75']])
pca_F = pca.fit_transform(train_2[['FNOX','FOXID','FSO4']])
pca_Z = pca.fit_transform(train_2[['FTBN','ZN']])
train_2=train_2.drop(['U25','U20','U14','U100','U75','U6','U4','FNOX','FOXID','FSO4','FTBN','ZN','S'],axis=1)
train_2[['U1','U2']]=pca_U1
train_2['U3']=pca_U2
train_2['F']=pca_F
train_2['Z']=pca_Z
train_2.columns
categorical_features = ['YEAR','COMPONENT_ARBITRARY']
test_stage_features = ['COMPONENT_ARBITRARY', 'ANONYMOUS_1', 'YEAR' , 'ANONYMOUS_2', 'AG', 'CO', 'CR', 'CU', 'H2O', 'MO', 'PQINDEX', 'V40']
train=train_2.copy()
all_X = train.drop(['ID', 'Y_LABEL'], axis = 1)
all_y = train['Y_LABEL']
test = test.drop(['ID','ZN','FE','MN','NI','TI','V'], axis = 1)
def get_values(value):
return value.values.reshape(-1, 1)
for col in all_X.columns:
if col not in categorical_features:
scaler = StandardScaler()
all_X[col] = scaler.fit_transform(get_values(all_X[col]))
if col in test.columns:
test[col] = scaler.transform(get_values(test[col]))
le = LabelEncoder()
for col in categorical_features:
all_X[col] = le.fit_transform(all_X[col])
if col in test.columns:
test[col] = le.transform(test[col])
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
Sum_of_squared_distances = []
K = range(1,10)
for k in K:
km = KMeans(n_clusters=k)
km = km.fit(all_X)
Sum_of_squared_distances.append(km.inertia_)
plt.plot(K, Sum_of_squared_distances, 'bx-')
plt.xlabel('k')
plt.ylabel('Sum_of_squared_distances')
plt.title('Elbow Method For Optimal k')
plt.show()
kmeans = KMeans(
...: init="random",
...: n_clusters=2,
...: n_init=10,
...: max_iter=300,
...: random_state=42
...: )
kmeans.fit(all_X)
all_X['Cluster']=kmeans.labels_
train_X, val_X, train_y, val_y = train_test_split(all_X[test_stage_features], all_y, test_size=0.2, random_state=CFG['SEED'], stratify=all_y)
"""
Dataset
DataSet은 DataLoader를 통하여 data를 받아오는 역할을 합니다.
Dataset class는 전체 dataset을 구성하는 단계입니다.
input으로는 x(input feature)과 y(label)을 tensor로 넣어줍니다.
PyTorch의 TensorDataset은 tensor를 감싸는 Dataset입니다.
Dataset Method
init(self): 필요한 변수들을 선언합니다.
get_item(self, index): 만든 리스트의 index 에 해당하는 샘플을 데이터셋에서 불러옵니다.
전처리를 실행한 다음 tensor 자료형으로 바꾸어 리턴하는 구조입니다.
즉, 데이터셋에서 특정 1개의 샘플을 가져오는 함수입니다
len(self): 학습 데이터의 갯수를 반환합니다.
나의 해석: CustomDataset()은 입력 데이터의 모든 관측값을 하나씩 torch.Tensor 형태로 바꿔주는 것 같다.
"""
class CustomDataset(Dataset):
def __init__(self, data_X, data_y, distillation=False):
super(CustomDataset, self).__init__()
self.data_X = data_X
self.data_y = data_y
self.distillation = distillation
def __len__(self):
return len(self.data_X)
def __getitem__(self, index):
if self.distillation:
# 지식 증류 학습 시
teacher_X = torch.Tensor(self.data_X.iloc[index])
#teacher_X는 전체 X Feature를 가진 데이터의 관측값을 하나씩 torch.Tensor 형태로 바꿔준다.
student_X = torch.Tensor(self.data_X[test_stage_features].iloc[index])
#student_X는 일부 X Features(test_stage_features)를 가진 데이터의 관측값을 하나씩 torch.Tensor 형태로 바꿔준다.
y = self.data_y.values[index]
return teacher_X, student_X, y
else:
# 지식 증류 학습이 아닐때
if self.data_y is None: #data_y가 제공되지 않을때..
test_X = torch.Tensor(self.data_X.iloc[index])
#test_X는 전체 X Feature를 가진 데이터의 관측값을 하나씩 torch.Tensor 형태로 바꿔준다.
return test_X
else: #data_y가 제공될때..
teacher_X = torch.Tensor(self.data_X.iloc[index])
#teacher_X는 전체 X Feature를 가진 데이터의 관측값을 하나씩 torch.Tensor 형태로 바꿔준다.
y = self.data_y.values[index]
return teacher_X, y
train_dataset = CustomDataset(train_X, train_y, False) #train_X와 train_y의 각 관측값을 torch.Tensor 형태로 바꿨다.
val_dataset = CustomDataset(val_X, val_y, False) #val_X와 val_y의 각 관측값을 torch.Tensor 형태로 바꿨다.
"""
DataLoader
Dataset을 batch기반의 딥러닝모델 학습을 위해서 미니배치 형태로 만듭니다.
DataLoader를 통해 Dataset의 전체 데이터가 batch size로 slice되어 공급됩니다.
batch_size 는 각 minibatch의 크기 즉 한 번의 배치 안에 있는 샘플 사이즈를 말합니다.
shuffle 은 Epoch 마다 데이터셋을 섞어, 데이터가 학습되는 순서를 바꾸는 기능을 말합니다.
"""
train_loader = DataLoader(train_dataset, batch_size = CFG['BATCH_SIZE'], shuffle=True)
#train_dataset에서 Batch_Size(286개)씩 무작위로 추출해서 데이터를 묶었다.
#즉 286개의 데이터 덩어리가 여러개있음
val_loader = DataLoader(val_dataset, batch_size = CFG['BATCH_SIZE'], shuffle=False)
#val_dataset에서 Batch_size(286개)만큼 추출해서 데이터를 묶었다.
#즉 286개의 데이터 덩어리가 여러개있음
class Teacher(nn.Module):
def __init__(self):
super(Teacher, self).__init__()
self.classifier = nn.Sequential(
nn.Linear(in_features=len(train_X.columns), out_features=128),
nn.BatchNorm1d(128),
nn.LeakyReLU(),
nn.Linear(in_features=128, out_features=256),
nn.BatchNorm1d(256),
nn.LeakyReLU(),
nn.Linear(in_features=256, out_features=512),
nn.BatchNorm1d(512),
nn.LeakyReLU(),
nn.Linear(in_features=512, out_features=1024),
nn.BatchNorm1d(1024),
nn.LeakyReLU(),
nn.Linear(in_features=1024, out_features=512),
nn.BatchNorm1d(512),
nn.LeakyReLU(),
nn.Linear(in_features=512, out_features=256),
nn.BatchNorm1d(256),
nn.LeakyReLU(),
nn.Linear(in_features=256, out_features=128),
nn.BatchNorm1d(128),
nn.LeakyReLU(),
nn.Linear(in_features=128, out_features=1),
nn.Sigmoid()
)
def forward(self, x):
output = self.classifier(x)
return output
def train(model, optimizer, train_loader, val_loader, scheduler, device):
model.to(device) #model을 gpu에 연결해준다.
best_score = 0
best_model = None
criterion = nn.BCELoss().to(device)
#BCELoss는 이진 분류에서 사용한다.
#모델의 구조 상 마지막 Layer가 Sigmoid 혹은 Softmax로 되어 있는 경우 사용한다.
#즉, 모델의 출력이 각 라벨에 대한 확률값으로 구성되었을 때 사용이 가능하다.
for epoch in range(CFG["EPOCHS"]):
train_loss = []
model.train()
#함수에 들어간 모델을 학습시킨다
#for문에 train_loader가 들어갔기 때문에 미니배치 사이즈만큼 묶은 데이터의 수만큼
#iteration(반복)이 돌아갈 것이다.
#그만큼 파라미터의 업데이트가 일어난다.
for X, y in tqdm(train_loader):#tqdm():프로그램 진행상황을 그림으로 볼 수 있게 해주는 파이썬 라이브러리
X = X.float().to(device)
y = y.float().to(device)
optimizer.zero_grad()
#한번의 학습이 완료되어지면(즉, Iteration이 한번 끝나면) gradients를 항상 0으로 만들어 주어야한다. 따라서 gradients를 0으로 초기화한다.
y_pred = model(X) #Batch Size 크기인 데이터 X가 model에 들어가 예측한 결과(y_pred)가 나온다.
loss = criterion(y_pred, y.reshape(-1, 1)) #오차를 구한다.(BCELoss이다)
loss.backward() #오차를 랜덤탠서로 미분한다.
optimizer.step() #랜덤탠서로 미분한 값으로 파라미터를 업데이트한다.
train_loss.append(loss.item()) #train_loss에 오차에 대한 정보를 업데이트한다.
val_loss, val_score = validation_teacher(model, val_loader, criterion, device)
print(f'Epoch [{epoch}], Train Loss : [{np.mean(train_loss) :.5f}] Val Loss : [{np.mean(val_loss) :.5f}] Val F1 Score : [{val_score:.5f}]')
if scheduler is not None:
scheduler.step(val_score) #learning rate를 조정해준다
if best_score < val_score: #best_score보다 val_score가 더 크면?
best_model = model #best_model에 model을 갱신한다.
best_score = val_score #best_score에 val_score을 갱신한다
return best_model
def competition_metric(true, pred):
return f1_score(true, pred, average="macro")
def validation_teacher(model, val_loader, criterion, device):
model.eval() #테스트 데이터나 검증 데이터를 사용하여 모델을 평가할 때 사용된다.
val_loss = []
pred_labels = []
true_labels = []
threshold = 0.35
with torch.no_grad():
for X, y in tqdm(val_loader):
X = X.float().to(device)
y = y.float().to(device)
model_pred = model(X.to(device))
loss = criterion(model_pred, y.reshape(-1, 1))
val_loss.append(loss.item())
model_pred = model_pred.squeeze(1).to('cpu')
pred_labels += model_pred.tolist()
true_labels += y.tolist()
pred_labels = np.where(np.array(pred_labels) > threshold, 1, 0)
val_f1 = competition_metric(true_labels, pred_labels)
return val_loss, val_f1
"""
validation_teacher()
val_loader 역시 미니배치 사이즈의 덩어리 데이터들로 구성되어있다.
각 덩어리가 X,y에 들어가서 앞에서 구축된 model에 적용되면, 예측값인 model_pred가 나온다.
실제 y와 model_pred간의 loss를 구한다. 이 값들을 val_loss에 저장한다. 또한, model_pred는
0과 1로 구분해서 pred_labels에 저장한다.
결론적으로, competition_metric(그런데 f1 score만 나오는듯)과 전체 데이터에 대한 val_loss가 나온다.
"""
model = Teacher()
model.eval()
optimizer = torch.optim.Adam(model.parameters(), lr=CFG['LEARNING_RATE'])
scheduler = torch.optim.lr_scheduler.ReduceLROnPlateau(optimizer, mode='max', factor=0.5, patience=1, threshold_mode='abs',min_lr=1e-8, verbose=True)
"""
optimizer: gradient를 구해서 weight의 값을 변화시켜주는 역할을 한다
scheduler: Learning Rate를 수정해준다
"""
teacher_model = train(model, optimizer, train_loader, val_loader, scheduler, device)
class Student(nn.Module):
def __init__(self):
super(Student, self).__init__()
self.classifier = nn.Sequential(
nn.Linear(in_features=len(test_stage_features), out_features=128),
nn.BatchNorm1d(128),
nn.LeakyReLU(),
nn.Linear(in_features=128, out_features=256),
nn.BatchNorm1d(256),
nn.LeakyReLU(),
nn.Linear(in_features=256, out_features=128),
nn.BatchNorm1d(128),
nn.LeakyReLU(),
nn.Linear(in_features=128, out_features=1),
nn.Sigmoid()
)
def forward(self, x):
output = self.classifier(x)
return output
def distillation(student_logits, labels, teacher_logits, alpha):
distillation_loss = nn.BCELoss()(student_logits, teacher_logits)
student_loss = nn.BCELoss()(student_logits, labels.reshape(-1, 1))
return alpha * student_loss + (1-alpha) * distillation_loss
def distill_loss(output, target, teacher_output, loss_fn=distillation, opt=optimizer):
loss_b = loss_fn(output, target, teacher_output, alpha=0.1)
"""
loss_b #loss_b는 단일값이 아니다!!!
distillation function에서 계산함
student_logits와 labels간의 차이를 계산한 student_loss와 student_logits와 teacher_logits의 차이를 계산한
distillation_loss를 연산하였다. alpha를 어떻게 조정하느냐에 따라서 값이 달라진다.
"""
if opt is not None:
opt.zero_grad() #gradients를 0으로 초기화한다.
loss_b.backward() #loss_b를 랜덤탠서로 미분한다.
opt.step() #랜덤탠서로 미분한 값으로 파라미터를 업데이트한다.
return loss_b.item()
def student_train(s_model, t_model, optimizer, train_loader, val_loader, scheduler, device):
s_model.to(device)
t_model.to(device)
best_score = 0
best_model = None
for epoch in range(CFG["EPOCHS"]):
train_loss = []
s_model.train()
t_model.eval()
for X_t, X_s, y in tqdm(train_loader):
X_t = X_t.float().to(device)
X_s = X_s.float().to(device)
y = y.float().to(device)
optimizer.zero_grad()
output = s_model(X_s) #미니배치 덩어리 X_s를 s_model(student model)에 넣은 결과
with torch.no_grad():
teacher_output = t_model(X_t) #미니배치 덩어리 X_t를 t_model(teacher model)에 넣은 결과
loss_b = distill_loss(output, y, teacher_output, loss_fn=distillation, opt=optimizer)
#distillation loss를 구한 결과
train_loss.append(loss_b)
#train_loss 에다가 각 배치의 loss_b를 append 한다.
val_loss, val_score = validation_student(s_model, t_model, val_loader, distill_loss, device)
print(f'Epoch [{epoch}], Train Loss : [{np.mean(train_loss) :.5f}] Val Loss : [{np.mean(val_loss) :.5f}] Val F1 Score : [{val_score:.5f}]')
#Epoch 당 train_loss의 평균, val_loss의 평균이 출력된다.
if scheduler is not None:
scheduler.step(val_score)
if best_score < val_score:
best_model = s_model
best_score = val_score
return best_model
def validation_student(s_model, t_model, val_loader, criterion, device):
s_model.eval()
t_model.eval()
val_loss = []
pred_labels = []
true_labels = []
threshold = 0.35
with torch.no_grad():
for X_t, X_s, y in tqdm(val_loader):
X_t = X_t.float().to(device)
X_s = X_s.float().to(device)
y = y.float().to(device)
model_pred = s_model(X_s)
teacher_output = t_model(X_t)
loss_b = distill_loss(model_pred, y, teacher_output, loss_fn=distillation, opt=None)
val_loss.append(loss_b)
model_pred = model_pred.squeeze(1).to('cpu')
pred_labels += model_pred.tolist()
true_labels += y.tolist()
pred_labels = np.where(np.array(pred_labels) > threshold, 1, 0)
val_f1 = competition_metric(true_labels, pred_labels)
return val_loss, val_f1
train_dataset = CustomDataset(train_X, train_y, True)
val_dataset = CustomDataset(val_X, val_y, True)
train_loader = DataLoader(train_dataset, batch_size = CFG['BATCH_SIZE'], shuffle=True)
val_loader = DataLoader(val_dataset, batch_size = CFG['BATCH_SIZE'], shuffle=False)
student_model = Student()
student_model.eval()
optimizer = torch.optim.Adam(student_model.parameters(), lr=CFG['LEARNING_RATE'])
scheduler = torch.optim.lr_scheduler.ReduceLROnPlateau(optimizer, mode='max', factor=0.5, patience=1, threshold_mode='abs',min_lr=1e-8, verbose=True)
#lr_scheduler: 학습률을 조정해주는 scheduler이다.
best_student_model = student_train(student_model, teacher_model, optimizer, train_loader, val_loader, scheduler, device)
val_dataset = CustomDataset(val_X, val_y, True)
val_loader = DataLoader(val_dataset, batch_size = CFG['BATCH_SIZE'], shuffle=False)
def choose_threshold(model, val_loader, device):
model.to(device)
model.eval()
thresholds = [0.05,0.06,0.07,0.08,0.09,0.1,0.11,0.12,0.129,0.13,0.131,0.1389,0.139,0.1391,0.14,0.141,0.149,0.15,0.151,0.1519,0.152,0.1521,0.153,0.179,0.18,0.181,0.189,0.19,0.191,0.198,0.199,0.2,0.209,0.21,0.211,0.22, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5]
pred_labels = []
true_labels = []
best_score = 0
best_thr = None
with torch.no_grad():
for _, x_s, y in tqdm(iter(val_loader)):
x_s = x_s.float().to(device)
y = y.float().to(device)
model_pred = model(x_s)
model_pred = model_pred.squeeze(1).to('cpu')
pred_labels += model_pred.tolist()
true_labels += y.tolist()
for threshold in thresholds:
pred_labels_thr = np.where(np.array(pred_labels) > threshold, 1, 0)
score_thr = competition_metric(true_labels, pred_labels_thr)
if best_score < score_thr:
best_score = score_thr
best_thr = threshold
return best_thr, best_score
best_threshold, best_score = choose_threshold(best_student_model, val_loader, device)
print(f'Best Threshold : [{best_threshold}], Score : [{best_score:.5f}]')
test_datasets = CustomDataset(test, None, False)
test_loaders = DataLoader(test_datasets, batch_size = CFG['BATCH_SIZE'], shuffle=False)
def inference(model, test_loader, threshold, device):
model.to(device)
model.eval()
test_predict = []
with torch.no_grad():
for x in tqdm(test_loader):
x = x.float().to(device)
model_pred = model(x)
model_pred = model_pred.squeeze(1).to('cpu')
test_predict += model_pred
test_predict = np.where(np.array(test_predict) > threshold, 1, 0)
print('Done.')
return test_predict
preds11 = inference(best_student_model, test_loaders, best_threshold, device)
test_loaders
from collections import Counter
Counter(preds11)
submission['Y_LABEL'] = preds11
submission.to_csv('12_12_2.csv',index=False)
"""
Pytorch 설명 출처: https://wikidocs.net/156998
"""
안녕하세요. 그동안 여러 활동들을 하다보니 블로그를 안하게 되었는데, 오랜만에 들어오니 많은 사람들이 저의 게시글을 읽어주시고 도움이 되셨다는 말씀에 감동을 받았습니다.
앞으로 제가 그동안 활동하며 사용한 여러 AI 이론들 (지식 증류 모델, 베이지안 최적화 등)을 다뤄볼 예정입니다.
기대해주세요.
근데.. 아마 6월 말에 올라올지도.. 너무 어려워서.. 흑
그래도.. 제 블로그에 와주셔서 감사합니다.
이 게시글은 책 '구글 BERT의 정석'의 셀프어텐션 설명을 요약 및 정리했습니다.
http://www.yes24.com/Product/Goods/104491152
구글 BERT의 정석 - YES24
인간보다 언어를 더 잘 이해하고 구현하는 고성능 AI 언어 모델 BERT이 책은 자연어 응용 분야에서 상당한 성능 향상을 이뤄 주목받고 있는 BERT 모델을 기초부터 다양한 변형 모델, 응용 사례까지
www.yes24.com
오늘은 셀프 어텐션에 대하여 알아볼 것입니다.
셀프 어텐션은 트랜스포머를 구성하는 핵심 요소입니다.
셀프 어텐션 -> 멀티 헤드 어텐션 -> 트랜스포머 순서로 향후 게시글을 올릴 예정입니다.
셀프 어텐션이 무엇인지 예를 통해서 알아보고, 사용되는 주요 행렬을 알아본 후, 작동 원리를 설명하면서 마무리하겠습니다.
셀프 어텐션은 트랜스포머를 구성하는 핵심 요소로, 특수한 형태의 어텐션입니다.
아래와 같은 문장이 있다고 가정합시다.
A cat ate the fish because it was hungry.
이 문장에서 우리는 'it'은 'cat'을 가리킴을 알 수 있습니다. 위 문장에 셀프 어텐션을 적용한다면, 모델은 'it'이 'fish'보다 'cat'과 연관성이 큰 것을 알 수 있습니다. 왜냐하면 이 문장이 모델에 입력되었을 때, 모델이 'it'이라는 단어의 의미를 이해하기 위해 문장 안에 있는 모든 단어와 'it'이라는 단어의 관계를 계산하는 작업을 수행하기 때문입니다.
그림으로 표현하면 아래와 같습니다.
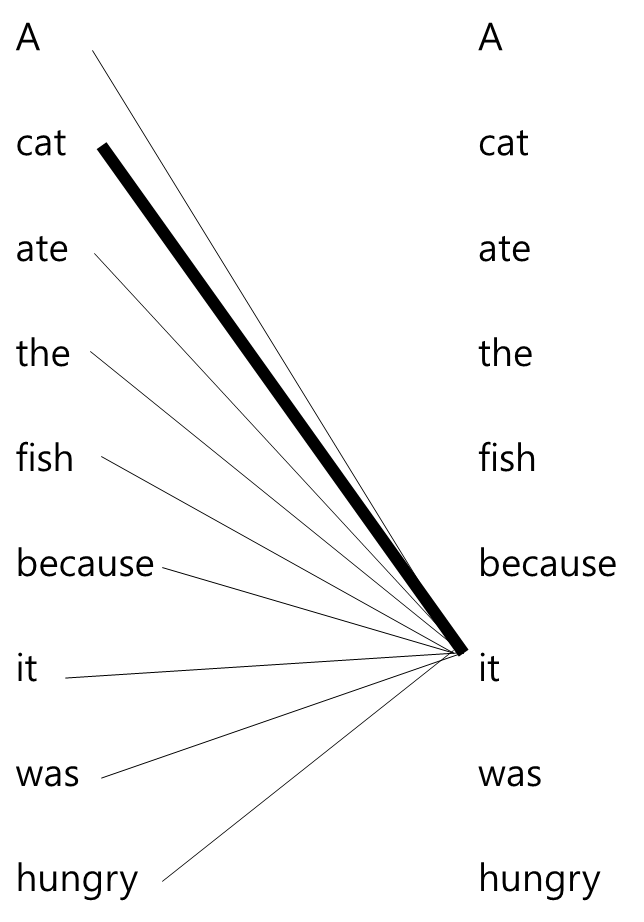
그림은 'it'이라는 단어의 표현을 계산하기 위해 'it'을 문장의 모든 단어와 연결하는 작업을 보여줍니다. 이와 같은 연결 작업으로 모델은 'it'이 'fish'보다 'cat'과 연관성이 큰 것을 학습합니다.
이렇게 작동하려면 무엇이 필요할까요? 셀프 어텐션에서 사용되는 주요 행렬에 대하여 알아봅시다.
문장을 셀프 어텐션에서 사용하려면 임베딩하는 작업이 필요합니다. 셀프 어텐션은 임베딩 된 벡터로부터 쿼리(Q) 행렬, 키(K) 행렬, 밸류(V) 행렬을 생성하고, 이 세 가지 행렬을 이용해서 작동합니다.
세 가지 행렬이 어떻게 만들어지는지 아래의 문장을 통해 설명드리겠습니다.
I am good
이 문장을 임베딩한 결과는 다음과 같습니다.

이 행렬을 X라고 하겠습니다. 행렬 X에서 첫 번째 행은 'I'의 임베딩, 두 번째 행은 'am'의 임베딩, 세 번째 행은 'good'의 임베딩을 의미합니다. 이때 X의 차원은 [문장 길이 x 임베딩 차원]의 형태입니다.
이렇게 임베딩 된 행렬로부터 세 개의 가중치 행렬을 행렬 X에 곱하면 쿼리 행렬, 키 행렬, 밸류 행렬이 계산됩니다. 여기서 세 개의 가중치 행렬은 처음에 임의의 값을 가지며, 학습 과정에서 최적의 값을 얻게 됩니다.
그림으로 표현하면 다음과 같습니다.
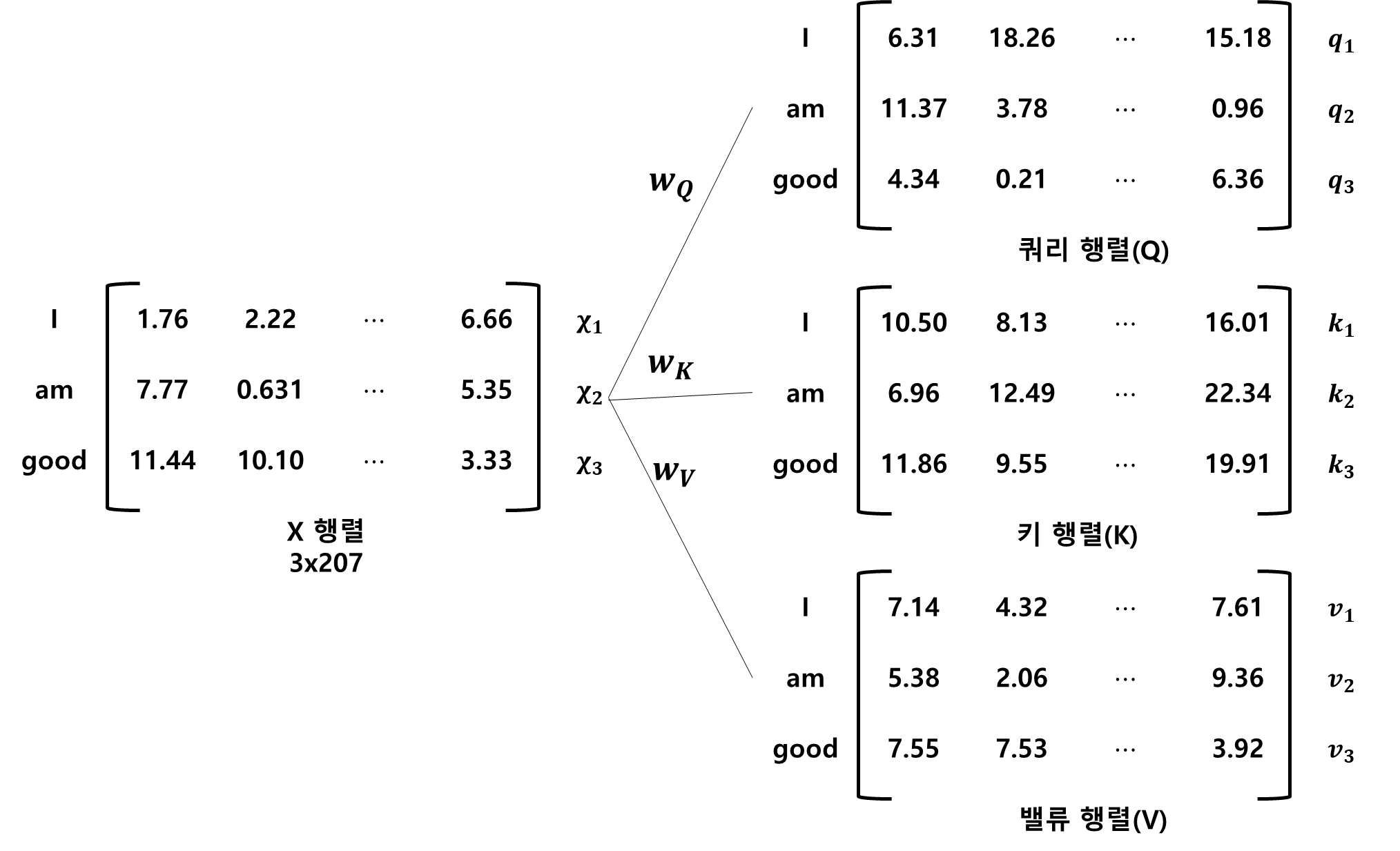
이제 쿼리, 키 밸류 행렬을 셀프 어텐션에 어떻게 사용하는지 보겠습니다.
셀프 어텐션은 총 4단계로 이루어져 있습니다.
1단계.
쿼리(Q) 행렬과 키(K) 행렬의 내적 연산을 수행합니다.

이를 해석하자면, Q와 K를 내적한 행렬(QK행렬)의 첫 번째 행은 쿼리 벡터1과 키 벡터 1, 2, 3의 내적을 계산한다는 것을 알 수 있습니다. 두 벡터 사이의 내적을 계산하면 두 벡터가 얼마나 유사한지를 알 수 있습니다. 즉, I의 쿼리 벡터와 I의 키 벡터, am의 키 벡터, good의 키 벡터 사이의 유사도를 계산한 것입니다.
QK행렬의 첫 번째 행은 110, 90, 80 입니다. 이를 통해 단어 I는 단어 am과 good보다 자신(I)과 연관성이 더 높은 것을 알 수 있습니다. 내적값이 110으로 첫번째 행에서 가장 높기 때문입니다.
2단계.
QK행렬의 키 벡터 차원의 제곱근값으로 나눕니다. 이렇게 하면, 안정적인 경사값을 얻을 수 있습니다.
키 벡터의 차원을 64라고 가정하면 이것의 제곱근인 8로 QK행렬을 나눕니다. 결과는 아래와 같습니다.

3단계.
이전 단계에서 계산한 유사도 값은 비정규화된 형태이기 때문에 소프트맥스 함수를 적용해 정규화 작업을 진행합니다.
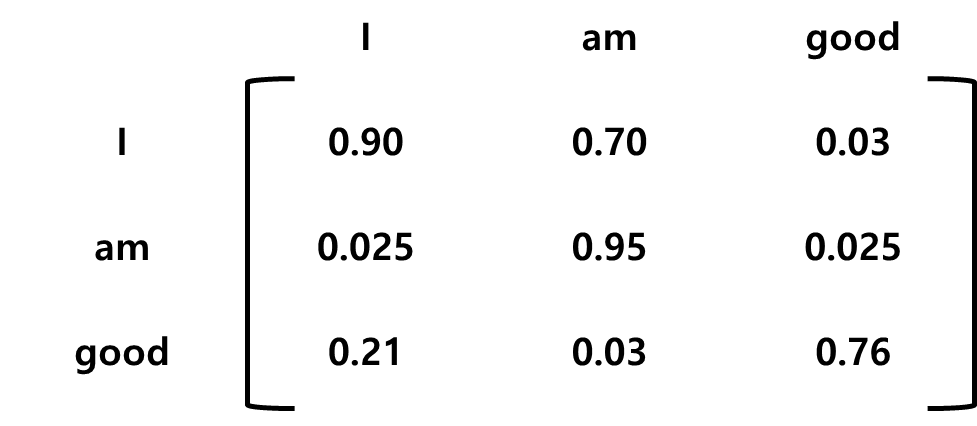
4단계.
앞에서 구한 행렬들을 이용하여 어텐션 행렬(Z)를 계산합니다. 어텐션 행렬은 문장의 각 단어의 벡터값을 갖습니다. 3단계에서 계산한 행렬에 밸류 행렬(V)를 곱하면 어텐션 행렬(Z)를 구할 수 있습니다.

Z를 구하면 단어 good의 셀프 어텐션 z3도 구할 수 있습니다.

z3는 밸류 벡터 v(I)의 0.21 비중, 벨류 벡터 v(am)의 0.03 비중, 벨류 벡터 v(good)의 0.76 비중의 합이라는 것을 알 수 있습니다. 이렇게 보면, 단어 good의 셀프 벡터값은 밸류 벡터 v(am)보다 v(I)가 많이 반영된 결과로 볼 수 있습니다. 이는 모델에서 good이 am이 아닌 I와 관련이 크다는 것을 알 수 있습니다. 셀프 어텐션 방법을 적용하면 이렇게 단어가 문장 내에 있는 다른 단어와 얼마나 연관성이 있는지를 알 수 있습니다.
정리하자면 다음과 같습니다.
1단계. 쿼리 행렬과 키 행렬 간의 내적을 계산하고 유사도를 구한다.
2단계. 1단계에서 구한 QK행렬을 키 행렬 차원의 제곱근으로 나눈다.
3단계. 2단계에서 구한 행렬에 소프트맥스 함수를 적용해 정규화 작업을 진행한다.
4단계. 마지막으로 밸류 행렬을 곱해 어텐션 행렬 Z를 산출한다.
| [LSTM] LSTM을 알아봅시다[밑바닥부터 시작하는 딥러닝2 참고]-I am yumida (0) | 2022.01.16 |
|---|---|
| [RNN] RNN을 알아봅시다[밑바닥부터 시작하는 딥러닝2 참고]-I am yumida (1) | 2022.01.16 |
| [RNN] RNN에 들어가기 전에..(밑바닥부터 시작하는 딥러닝2) - I am yumida (0) | 2021.12.30 |
| 경사하강법에 대하여 알아봅시다.(Do it! 딥러닝 입문 정리) - I am yumida (0) | 2021.08.18 |
| MNIST 데이터를 CNN에 적용하여 분류하기 - I am yumida (0) | 2021.08.12 |
카운팅 정렬은 계산 복잡성이 O(n)인 알고리즘입니다.
이 게시글은 아래의 블로그를 참고했습니다. 감사합니다.
https://elrion018.tistory.com/37
카운팅 정렬(counting sort) - 정렬 알고리즘, 파이썬
지금까지 배워온 정렬은 두 수의 대소를 '비교'하는 과정을 거쳐 정렬하는 comparison sort였습니다. 두 수를 반복적으로 비교해 정렬하는 comparison sort는 아무리 알고리즘을 잘 짜도 계산 복잡성이 O(
elrion018.tistory.com
카운팅 정렬 코드는 다음과 같습니다.
def counting_sort(array,max):
counting_array = [0]*(max+1)
for i in array:
counting_array[i] += 1
for i in range(max):
counting_array[i+1] += counting_array[i]
output_array = [-1]*len(array)
for i in array:
output_array[counting_array[i] -1] = i
counting_array[i] -= 1
return output_array
10개의 array [5,5,2,2,4,3,3,1,1,7]가 존재합니다. 이것을 정렬하기 위해 counting_array 와 output_array가 필요합니다.
1. 우선 counting_array는 array의 누적 빈도수를 의미합니다. 이것을 구해봅시다.
1) 처음에는 빈도수를 구하기 위해 0이 8개(array 의 최대값+1)인 리스트를 생성합니다.
counting_array=[0,0,0,0,0,0,0,0]
2) 빈도수를 구합니다.
counting_array = [0,2,2,2,1,2,0,1] (array의 빈도수) -> 0이 0개있고,1이 2개있고,..., 6이 0개 있고, 7이 1개 있는 것입니다.
3) 누적 빈도수를 구합니다.
counting_array = [0,2,4,6,7,9,9,10] (array의 누적 빈도수)
2. output_array를 구합니다. 여기에서 처음 주어진 array가 정렬된 결과값이 나옵니다.
1) 우선 -1을 array 개수만큼 리스트로 설정합니다.
output_array=[-1,-1,-1,-1,-1,-1,-1,-1,-1,-1] (output_array의 초기설정)
2) counting_array와 엮어서 output_array를 구해보겠습니다.(CODE를 이용해 설명하겠습니다)
CODE
for i in array:
output_array[counting_array[i] -1] = i
counting_array[i] -= 1
- array의 첫번째 원소가 5일 때, counting_array[5]는 5일때의 누적빈도수를 의미합니다.
누적빈도수가 9이기 때문에 output_array[8]은 5입니다.
counting_array[5]는 9에서 8로 줄어듭니다.
output_array=[-1,-1,-1,-1,-1,-1,-1,-1, 5,-1]
- array의 두번째 원소가 5일 때, counting_array[5]는 5일때의 누적빈도수를 의미합니다.
누적빈도수가 8이기 때문에 output_array[7]은 5입니다.
counting_array[5]는 8에서 7로 줄어듭니다.
output_array=[-1,-1,-1,-1, -1,-1,-1, 5, 5,-1]
- array의 세번째 원소가 2일 때, counting_array[2]은 2일때의 누적빈도수를 의미합니다.
누적빈도수가 4이기 때문에 output_array[3]은 2입니다.
counting_array[2]는 4에서 3으로 줄어듭니다.
output_array=[-1,-1,-1, 2, -1,-1, -1, 5, 5,-1]
- array의 네번째 원소가 2일 때, counting_array[2]은 2일때의 누적빈도수를 의미합니다.
누적빈도수가 3이기 때문에 output_array[2]는 2입니다.
counting_array[2]는 3에서 2로 줄어듭니다.
output_array=[-1,-1, 2, 2, -1,-1, -1, 5, 5,-1]
- array의 다섯번째 원소가 4일 때, counting_array[4]은 4일때의 누적빈도수를 의미합니다.
누적빈도수가 7이기 때문에 output_array[6]는 4입니다.
counting_array[4]는 7에서 6으로 줄어듭니다.
output_array=[-1,-1, 2, 2, -1, -1, 4, 5, 5,-1]
이와 같이 계산하면 output_array는 [1,1,2,2,3,3,3,4,5,5,7]로 정렬됩니다.
| [백준 11729] 하노이 탑 이동 순서 (0) | 2022.03.01 |
|---|---|
| [백준 #10066] 팰린드롬 (시간초과, 메모리초과.. 그저 기록용 코드) (0) | 2022.01.18 |
| [리트코드 #5] 가장 긴 팰린드롬 부분 문자열 (0) | 2022.01.17 |
| [알고리즘] DFS에 대해서 알아봅시다. - I am yumida (0) | 2021.12.31 |
| [알고리즘] BFS에 대해 알아봅시다. - I am yumida (0) | 2021.12.30 |
#이 문제는 풀지 못했다.. 심지어 이해하기도 힘들었다. 나같은 사람을 위해 코드를 해체해봤다.
https://www.acmicpc.net/problem/11729
11729번: 하노이 탑 이동 순서
세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로
www.acmicpc.net
def hanoi(n, a, b):
if n > 1: [과정A]
hanoi(n-1, a, 6-a-b)
print(a, b) [과정C]
if n > 1: [과정B]
hanoi(n-1, 6-a-b, b)
n = int(input())
print(2**n -1)
hanoi(n, 1, 3)
CODE의 맨 마지막 줄에 있는 hanoi(n,1,3)은 3개의 원반이 있을 때, 기둥1에서 기둥3으로 이동하는 것을 의미한다.
먼저 hanoi(3,1,3)으로 시작한다.

CODE의 [과정A]에 따르면 hanoi(2,1,2)가 되고, [과정C]에 따르면 print(1,3)가 된다. [과정B]에 따르면 hanoi(2,2,3)이 된다.
1. hanoi(2,1,2): 2개의 원반을 기둥1에서 기둥2로 옮긴다.

>>hanoi(2,1,2)는 [과정A]에 따르면 hanoi(1,1,3)이 되고, [과정C]에 따르면 print(1,2)이 된다. [과정B]에 따르면 hanoi(1,3,2)가 된다.
1) hanoi(1,1,3): 1개의 원반을 기둥1에서 기둥3으로 옮긴다. 1번째 출력: print(1,3)

2) print(1,2): 1개의 원반을 기둥1에서 기둥2로 옮긴다. 2번째 출력: print(1,2)

3) hanoi(1,3,2): 1개의 원반을 기둥3에서 기둥2로 옮긴다. 3번째 출력: print(3,2)

최종적으로 hanoi(2,1,2) 결과, 2개의 원반이 기둥1에서 기둥2로 옮겨졌다.
2. print(1,3): 나머지 1개의 원반을 기둥1에서 기둥3으로 옮긴다. 4번째 출력: print(1,3)

3. hanoi(2,2,3): 2개의 원반을 기둥2에서 기둥3으로 옮긴다.

>>hanoi(2,2,3)는 [과정A]에 따르면 hanoi(1,2,1)이 되고, [과정C]에 따르면 print(2,3)이 된다. [과정B]에 따르면 hanoi(1,1,3)이 된다.
1) hanoi(1,2,1): 1개의 원반을 기둥2에서 기둥1로 옮긴다. 5번째 출력: print(2,1)

2) print(2,3): 1개의 원반을 기둥2에서 기둥3로 옮긴다. 6번째 출력: print(2,3)

3) hanoi(1,1,3): 1개의 원반을 기둥1에서 기둥3로 옮긴다. 7번째 출력: print(1,3)
| [파이썬] 카운팅 정렬 (0) | 2022.03.03 |
|---|---|
| [백준 #10066] 팰린드롬 (시간초과, 메모리초과.. 그저 기록용 코드) (0) | 2022.01.18 |
| [리트코드 #5] 가장 긴 팰린드롬 부분 문자열 (0) | 2022.01.17 |
| [알고리즘] DFS에 대해서 알아봅시다. - I am yumida (0) | 2021.12.31 |
| [알고리즘] BFS에 대해 알아봅시다. - I am yumida (0) | 2021.12.30 |